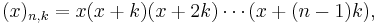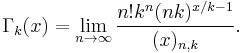Pochhammer k-symbol

In the mathematical theory of special functions, the Pochhammer k-symbol and the k-gamma function, introduced by Rafael Díaz and Eddy Pariguan[1], are generalizations of the Pochhammer symbol and gamma function. They differ from the Pochhammer symbol and gamma function in that they can be related to a general arithmetic progression in the same manner as those are related to the sequence of consecutive integers.

The Pochhammer k-symbol (x)n,k is defined as

(x)_{n,k} = x(x %2B k)(x %2B 2k) \cdots (x %2B (n-1)k),\,

and the k-gamma function Γk, with k > 0, is defined as

\Gamma_k(x) = \lim_{n\to\infty} \frac{n!k^n (nk)^{x/k - 1}}{(x)_{n,k}}.

When k = 1 the standard Pochhammer symbol and gamma function are obtained.

Díaz and Pariguan use these definitions to demonstrate a number of properties of the hypergeometric function. Although Díaz and Pariguan restrict these symbols to k > 0, the Pochhammer k-symbol as they define it is well-defined for all real k, and for negative k gives the falling factorial, while for k = 0 it reduces to the power xn.

The Díaz and Pariguan paper does not address the many analogies between the Pochhammer k-symbol and the power function, such as the fact that the binomial theorem can be extended to Pochhammer k-symbols. It is true, however, that many equations involving the power function xn continue to hold when xn is replaced by (x)n,k.

References

  1. ^ Díaz, Rafael; Eddy Pariguan (2005). "On hypergeometric functions and k-Pochhammer symbol". arXiv:math/0405596 [math.CA].